動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru1.式の乗法・除法 ≪復習≫ 単項式・多項式の意味 数や文字についての乗法だけでできている式を単項式 とい います。1つの文字や式も単項式と考えます。 5a ,ab , ,30 ,a2 ,-a ,-abcd2 単項式の和の形で表された式を多項式といいます。 文字が多いし、途中式が複雑だし、よくわかりません! というわけで、今回の記事では中2で学習する式の計算の単元から「単項式の乗法・除法の解き方」についてイチからサクッと解説していきます。 覚えるルールは少ないから、計算の手順を身につけていこう! 動画でサクッと理解したい方はこちら! 中2単項式の乗法・除法の解き方をイチから

高校数学 組立除法による整式の割り算 受験の月
多項式の除法 問題
多項式の除法 問題- 分数式の乗法では、 分母どうし、分子どうし をそれぞれ掛け算 します。 分数式の除法では、 割る数式の逆数 を割られる数式に掛け算 します。 分数式の基本性質や乗法・除法の計算については、すでに学習していることなので今更と思うかもしれません。 今回は「多項式の除法」です。 中学数学でやっているような気がするのに、意外に一度もやっていないのが、多項式の除法です。 これは筆算していくことができます。 やり方・考え方は数字のわり算の筆算と同じです。 6 )764




多項式の除法 数学ii フリー教材開発コミュニティ Ftext
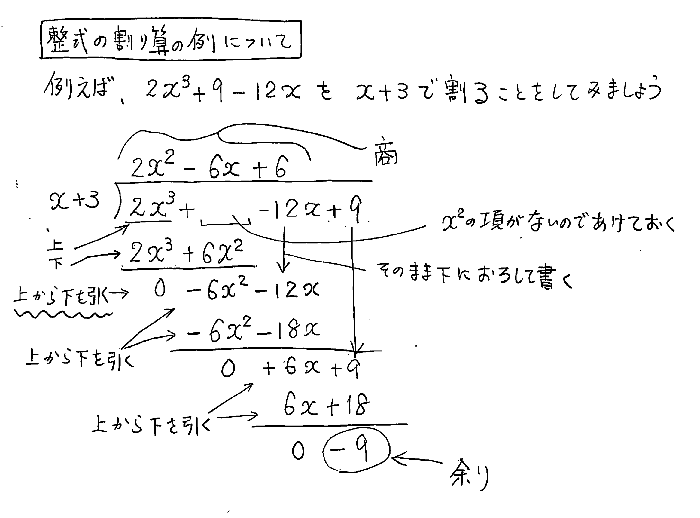
整数の除法に続き,今度は多項式の除法(polynomial division)について考えてみる. たとえば,「$x^3 – x^2 2x – 3$を$x^2 2x – 1$で割る」とは \begin{align} &x^3x^22x3\\ =&(x^22x1)Q(x)r(x) \end{align} と変形することであると定義する.その他の動画 数学 1 多項式の計算 1 単項式と多項式の乗法、除法 数学 1 多項式の計算 2 多項式の乗法 数学 1 多項式の計算次は多項式と単項式の除法についてです。 多項式と数の除法についてはすでに学習していて、2つのアプローチ方法で計算することができました。 1 分数になおして計算する 2 乗法(かけ算)になおして計算する ( 6 a 2 − 8 a b) ÷ 2 a = 6 a 2 2 a − 8 a b 2 a = 3
Share your videos with friends, family, and the world多項式は既約な多項式の積として, 定数倍と順序を除けばただ一通りに表すことができる. 多項式の場合も 素因数分解の一意性 という. 基本的な定理である.中3 多項式と単項式の乗法除法 5x (4x3y) = 5x×4x5x× (3y) = x215xy (6a2b15ab2)÷ 3 2 ab = (6a2b15ab2)× 2 3ab
単元 式の展開と因数分解 (啓林館) 1 多項式の計算 ・1・ 式の乗法、除法 全4時間2乗比較 ← PC用は別頁 == 多項式の除法(割り算) == 解説 ここだけの話 このページでは,話をわかりやすくするために 37 のような数字では上の位の数字( 3 )を 親分 ,下の位の数字( 7 )を 子分 とする. また, 3x7 のような多項式では,次数の高い方( 3x )を 親分 ,次数の低い方( 7 )を 子分 とする. 2x25x−1 のような2次式では, 親分 は 2x2 , 子分多項式と単項式の乗法と除法 単項式に多項式をかける乗法は、分配法則を使ってかっこを外して計算する。 1 次の計算をしなさい。 a (bc)= ab ac ( a b )÷c =( a b )× = 多項式を単項式でわる除法は、わる式の逆数をかけて計算する。




単項式の全てがこれでわかる 単項式の係数と次数 乗法 除法や多項式との違いまで 高校生向け受験応援メディア 受験のミカタ




式の計算 多項式の乗法と除法の計算の解き方とは は に変えて後ろの数を逆数にする 中学数学をはじめから分かりやすく
多項式の除法を筆算する際、主に2つの方法が用いられる。 1つ目は整数除算の筆算でお馴染みの 長除法 、2つ目はそれを簡略化した 組立除法 である。多項式の除法は,話をわかりやすくするために 37 のような數字では上の位の數字( 3 )を親分,②単項式の乗法,実は考え方は「整數の割り算」とほとんど同じで,ぜひこちら 多項式の割り算計算機 – 多項式の除法には、3つのやり方があります。 まず、 ①一般的な除法と同じように筆算する方法 、そして、 ②恒等式を用いて解く方法 、最後に、少しむずかしいですが ③組立除法 の3つで




多項式の除法 数学ii フリー教材開発コミュニティ Ftext




例題で学ぶ高校数学 整式の割り算
多項式と単項式の乗法と除法について学ぼう! 3年 1章 式の展開と因数分解2/9 教P1617( )年( )組( )名前 ★ 多項式×多項式 の計算では,分配法則をくり返し使えば,除法の原理(じょほうのげんり、英 division theorem )とは、「被除数と除数と呼ばれる二つの自然数に対して、商と剰余と呼ばれる二つの自然数が、与えられた性質を満たして一意に定まる」ことを示す算術における定理である。 たとえば、自然数 n および 0 でない自然数 m に対して、 n = am多項式の除法 多項式 f(x) , g(x) において f(x) = g(x)Q(x) r(x) (deg r(x) < deg g(x)) と変形できたとき, Q(x) を商, r(x) を余りという. 特に,余り r(x) が 0 のとき, f(x) は g(x) で割り切れるという. さきほどの例では,商 Q(x) は x– 3 ,余り r(x) は 9x– 6 となる.つまり x3 − x2 2x − 3 = (x2 2x − 1) × (x − 3) (9x − 6) となる.各自,以下の2点について確認しておこう




1 3 5多項式除法 多項除以多項 Youtube




多項式除法の筆算の長除法と組立除法 Limg Note
Part 1 1 変数多項式の割り算> 1 つの多項式での割り算 Part 1 1変数多項式の割り算 11 1つの多項式での割り算 C 複素数全体のなす集合 Cx = fadxd a1x a0 j ad;;a1;a0 2 Cg 複素数係数の1変数多項式全体のなす集合 0でない多項式f(x) = adxd a1x a0(ad ̸= 0 )に対し 除法定理(多項式版)を繰り返し使ってみよう 任意の多項式\(f(x)\)を,1次の多項式\(x\alpha\)で割ることを考えます 除法定理から,以下の式を満たす多項式\(Q_1(x), R_1(x)\)が(\(f(x)\),\(x\alpha\)に対して)一意に存在します $${ f(x) = (x\alpha) \cdot Q_1(x) R_1(x) }$$数3年 多項式の乗法と除法 解 答 名前 /点 1 次の計算をせよ。 ⑴ 5a( 4a-b) ⑵ 16x( 1 2 x- 5 8 y) ⑶ (x2y-9xy)÷(-xy) ⑷ (8a2b-24ab-28a)÷4a ⑸ 4a( 5a-2b)-3a( a-4b) ⑹ x( x+2) 3 - x( 6x+5) 9 次の式を展開せよ。




数学 中2 7 単項式の乗法 除法 Youtube



ユックリードの互除法と多項式 すごいや 公約どおり本当にあったんだ 希望的観測日記 ブログ枝部
多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後多項式と数の除法 次の計算をしましょう。 問題集の無料ダウンロードサイトは「おかわりドリル」で検索 https//wwwokadorinet 多項式 a, b a,b a, b が与えられたときに割り算を実行する( q, r q,r q, r を求める)二通りの方法を解説します。 deg A < deg B \deg A




整式の除法の練習問題 割り算のやり方 数学ii By ふぇるまー マナペディア




式と証明 整式の割り算について 日々是鍛錬 ひびこれたんれん
2 小テスト 実施日 年 月 日 中数3 年 組 番 名前 1 次の式を展開しなさい。 ⑴ (x -1)(y+5) -=xy+5x-y 5 ⑵ (7x -4y)(2x -y) -=14x2 15xy+4y2 ⑶ (4a -2b -1)(3a -2b) =12a2-8ab-6ab+4 b2-3a+2 -=12 a2 14ab+4 b2-3 +2 1章 式の計算 1節 多項式の乗法と除法 組み立て除法とは,整式 $f(x)$ を $1$ 次式 $x\alpha$ で割ったときの商と余りを簡単に決定する方法です.整式の割り算は筆算を使えばもちろん答えが求まります.しかし,整式を $1$ 次式で割る場合には組み立て除法が使えます.慣れれば筆算を行うより,組立除法の方が圧倒的に早くできるので,便利です. 5:単項式の除法 単項式の乗法を学習した後は、単項式の除法(割り算)を学習しましょう。 では、早速例を見てみます。 例1 4x 3 y 5 ÷ 2x 2 y 3 = 2x 32 y 53 = 2xy 2 ・・・(答) 一般的に、文字の除法については、以下が成り立ちます。 a m ÷ a n =a mn




式と証明 割り算と整式の決定について 日々是鍛錬 ひびこれたんれん




多項式の除法とは 計算方法をわかりやすく解説して演習問題を解く 数学ia Himokuri
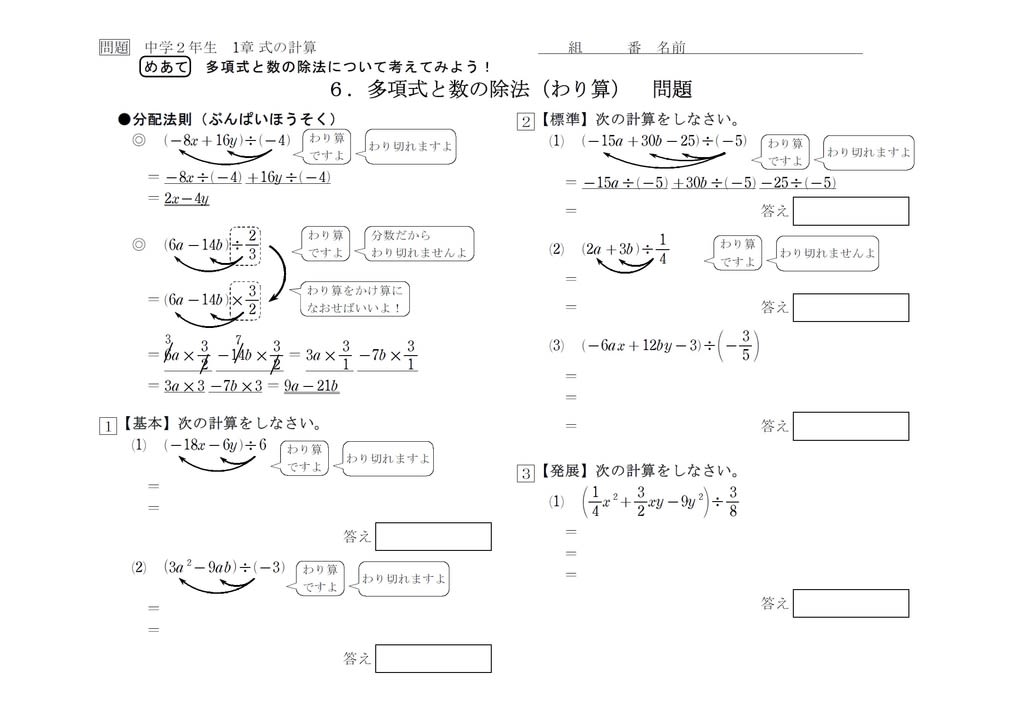
単項式と多項式の乗法・除法 (教科書p16~17) 学習の目標 単項式×多項式,多項式÷単項式の計算方法を学習しよう 1.単項式と多項式の乗法 (例1) ( − )×(− ) (= ×− )− ×(− ) ×(− ) =− −数学Gアップシ-ト 3年第1章 多項式(2) 3年1章 No.2 -多項式と単項式の除法の計算ができるようになろう- p9 学習日 月 日 年 組 番 氏名 復習しよう。 1 次の式の右辺の分子にあてはまる文字式を書多項式の乗法,除法① (教科書P) 学習の目標 分配法則を使って,多項式の乗法・除法を計算しよう 1.多項式と数の乗法 ★分配法則を使って計算する。 (例) 3(2 5 −1) =3×2 3×5y3×(−1) ←3を( )の中すべてにかけ算する =6 15 −3



3




Python實現多項式加減乘除 台部落
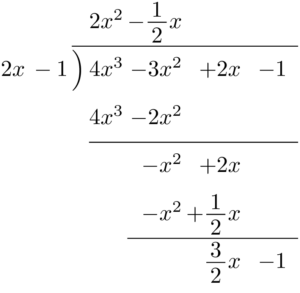
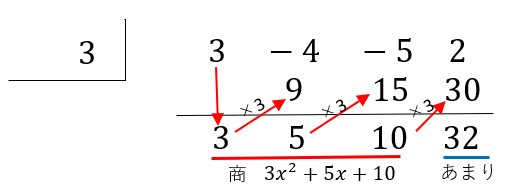
ここでは組立除法 (synthetic division) という計算方法について、やり方を説明します。 具体例で説明します。 多項式 \((3x^32x^27x2)\) を \((x\dfrac{1}{3})\) で割り算するにはどうしたらよいでしょうか。 組立除法を使わないで割り算する方法としては、まず直接、多項式同士の除算として次のよR の次数は g の次数よりも小さい。(ただし、定数多項式 0 の次数は 0 より小さいものと解釈する。)多項式と数の乗法、除法 分配法則 a (x y) = ax ay




多项式除法 维基百科 自由的百科全书



文字係数の整式の割り算
多項式の除法とは、体 K 上の(1変数)多項式 f, g (ただし g ≠ 0 )に対して、次の2条件をみたす多項式 Q, R を求める手続きである。 f = gQ R;こんにちは、ウチダです。 本記事では、中学数学の 「多項式と単項式の違い」 について、まずは次数についての理解をしていきましょう。 そのうえで、実際の計算、特に乗除(乗法除法)を分配法則を用いて行っていきます! 多項式と単項式の違いとは まずは言葉の定義を見てみましょうか。




いろいろな多項式の計算 ねらい 一次式と数の乗法 除法の計算ができる Ppt Download



数学 B 多項式の割り算 自治医科大 明治薬科大 ページ 2 大学入試数学の考え方と解法




中2数学 多項式の除法 わり算 練習編 映像授業のtry It トライイット



整式の除法とは 1分でわかる意味 商と余り 除法の等式 分数との関係




多項式除法計算器四次多項式除法計算器 Zzkvs



第1回 整式の計算 整式の割り算について




中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に



3 2第1章多項式 式の展開 単項式と多項式の除法




中学2年生 多項式の除法 公式 個別進学教室マナラボ受験 教育情報サイト




中学数学3年 単項式と多項式の乗法と除法 受験の月




数 式と証明 多項式の除法 3次式 1次式 オンライン無料塾 ターンナップ Youtube




整式の除法の練習問題 割り算のやり方 数学ii By ふぇるまー マナペディア




整式の除法 X 4x X 3を整式bで割ったときの商x 5 余が4x 7のとき Bを求める問題 数学ii By ふぇるまー マナペディア




國中數學第三冊ch1多項式除法之除法原理 Youtube
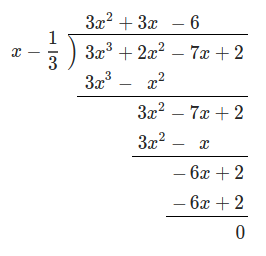



組立除法 初等数学 基礎からの数学入門



組み立て除法のやり方と原理 思考力を鍛える数学




多項式的除法 翰林雲端學院




C で多項式の除法をするプログラム 独り言はもうやめませんか




数学 整式の除法 場合の数 接線と法線 確率 早稲田大学 さくらの個別指導 さくら教育研究所 Skredu




中3 展開と因数分解2 多項式と単項式の除法 予習 中学数学の勉強に



Studydoctor多項式と単項式の乗法と除法 中3数学 Studydoctor




中学数学 多項式の計算 ママ塾ノート



21 章老師作一個多項式除法示範後 擦掉計算過程中的六個係數 並以a B C D 阿摩線上測驗




ユークリッドの互除法を多項式に拡張して Rustで 実装する Je6bmq S Diary




多項式と単項式の乗除 無料で使える中学学習プリント




高校数学 組立除法による整式の割り算 受験の月



1



多項式と数の乗法 除法について学ぼう Ppt Download




高校数学 B 整式の割り算を筆算なし 暗算で解く方法 やはり俺の考察ブログはまちがっている アニメ 数学



剰余の定理



組み立て除法のやり方と原理 思考力を鍛える数学




整式とは 整式の次数とは何か 整式の計算についても軽く解説します 遊ぶ数学




中学数学 多項式の計算 ママ塾ノート




超重要な 多項式の割り算 をイメージから掴もう




中学2年数学 式の計算 多項式と数の乗法 掛け算 除法 割り算 分配法則を使って計算しよう 数学の面白いこと 役に立つことをまとめたサイト




多項式の掛け算 割り算と分配法則 代入計算のやり方 リョースケ大学



3




多項式の除法 数学ii フリー教材開発コミュニティ Ftext



Studydoctor整式の除法 高校数 Studydoctor



整式に関する基礎的な定理 思考力を鍛える数学



整式の除法とは 1分でわかる意味 商と余り 除法の等式 分数との関係




翻轉學習影片 國中 數學 乘法公式與多項式 多項式的除法 練習2



多項式の割り算の二通りの計算方法と例題 高校数学の美しい物語




多项式除法 维基百科 自由的百科全书




整式の割り算の余り 剰余の定理 おいしい数学




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



高校数学 整式の除法による余りの求め方 筆算 剰余の定理 組立除法 学校よりわかりやすいサイト
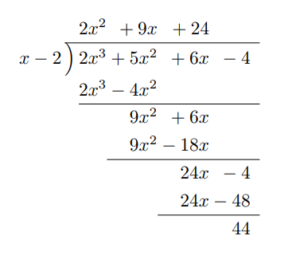



整式を商 あまりで表現する 高校数学の知識庫




多項式の除法 数学ii フリー教材開発コミュニティ Ftext
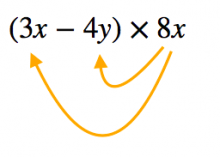



多項式と単項式 乗法 除法 苦手な数学を簡単に
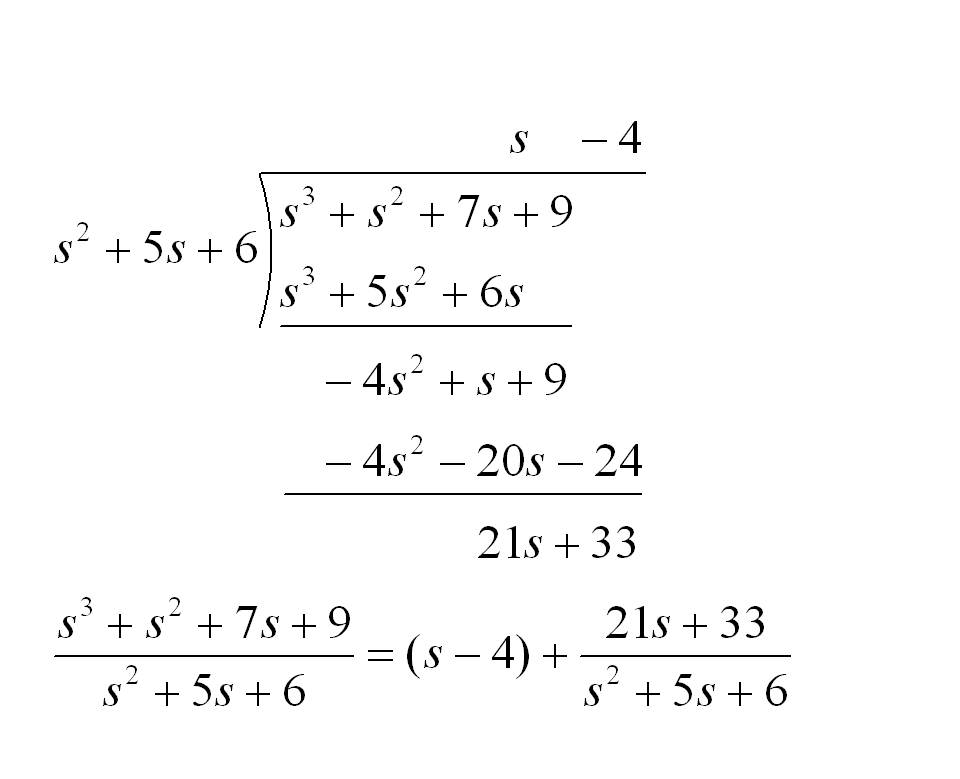



多項式除法 一般步驟 舉例 整除 套用 中文百科全書



組立除法 さぼりたいという気持ち キソカラ



2




整式の割り算 2種類以上の文字を含んだ整式の除法問題 数学ii By ふぇるまー マナペディア




数学 多項式の除法に関する問題 オンラインプロ家庭教師 理数ゼミ



文字係数の整式の割り算



48s96ub7b0z5f Net Kumitatejohou




1 3 4多項式除法 Youtube




新鮮な多項式 の 除法 最高のカラーリングのアイデア



多項式的除法運算 除法關係式 Live 多媒體數學觀念典online




多項式の除法 数学ii フリー教材開発コミュニティ Ftext




中学3年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学2年生 多項式の除法 公式 個別進学教室マナラボ受験 教育情報サイト




中学2年生 多項式の除法 公式 個別進学教室マナラボ受験 教育情報サイト



1




高校数学 整式の割り算 1次式で割る 映像授業のtry It トライイット
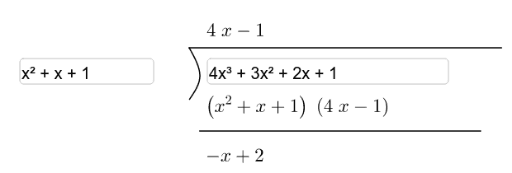



多項式の割り算計算機 Geogebra




式と証明 2つ以上の文字を含む整式の割り算について 日々是鍛錬 ひびこれたんれん




2 2a觀念03多項式的除法與除法原理 數學 均一教育平台




式と証明 整式の割り算について 日々是鍛錬 ひびこれたんれん




式と証明 2つ以上の文字を含む整式の割り算について 日々是鍛錬 ひびこれたんれん




中3数学 単項式 多項式の除法 例題編 映像授業のtry It トライイット




数学 B 多項式の割り算 自治医科大 明治薬科大 ページ 4 大学入試数学の考え方と解法




Kelas 9 Catatan Tentang 中3 数学 多項式の計算 Clear



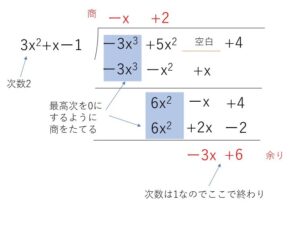
中2 式の計算6 動画 多項式の除法 わり算 発展の解説 中学数学の勉強に



割り算について成り立つ等式 商と余りの関係 割り算の原理




多項式の除法と微分係数と 鬼原数学ゼミ



整式の除法の基礎 教えて数学理科



多項式除法




山と数学 そして英語 数 式と証明 多項式の除法




整式の除法の練習問題 割り算のやり方 数学ii By ふぇるまー マナペディア




多項式と単項式の乗法 除法 教遊者
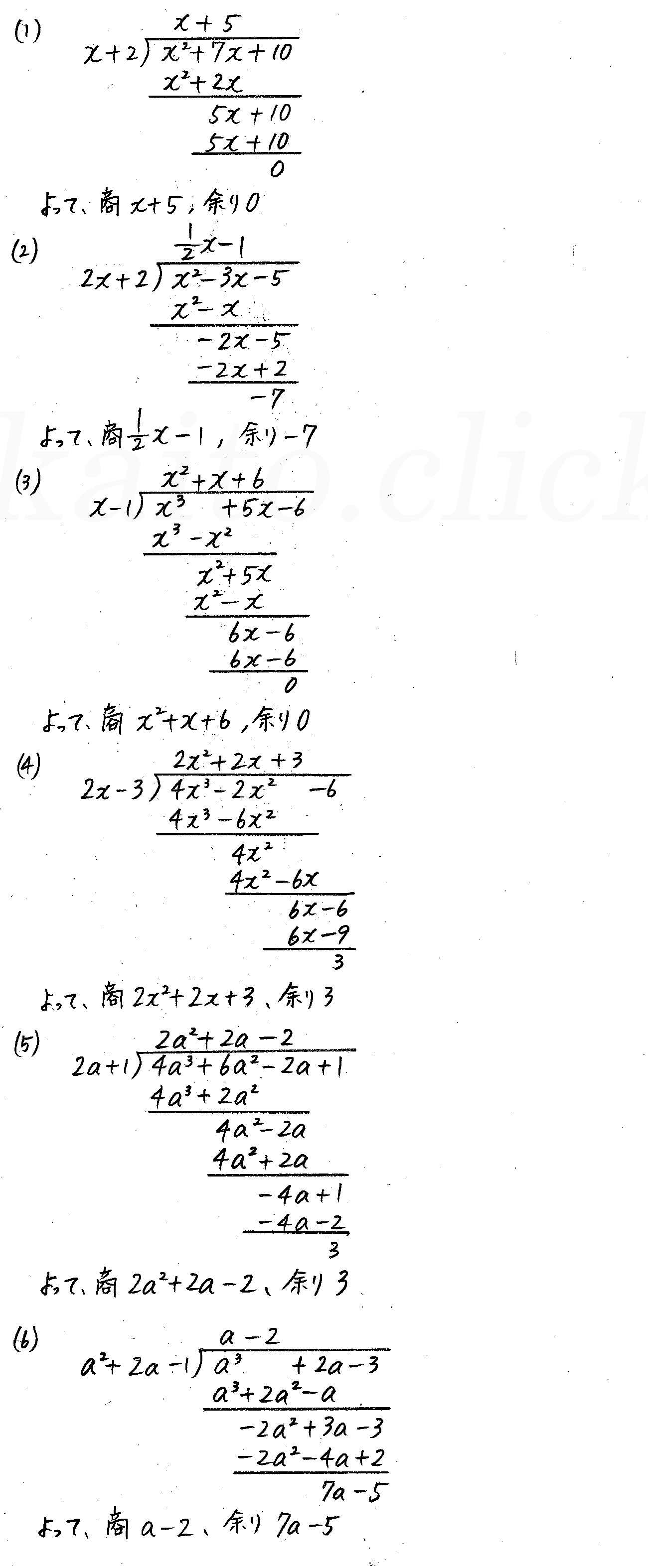



改訂版 4step数学 P10 3 整式の割り算




中2 数学 多項式と数の乗法 除法 中学生 数学のノート Clear
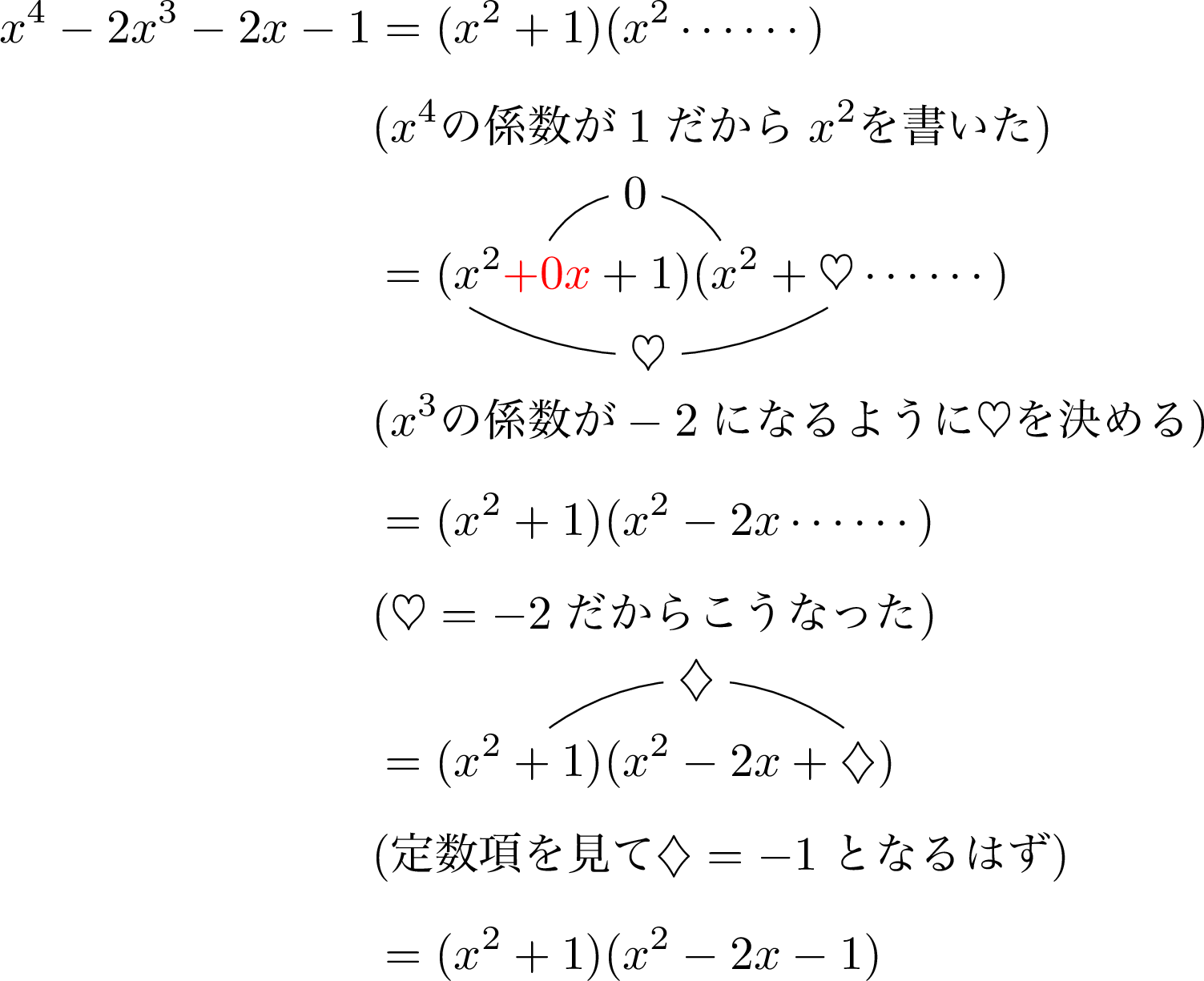



多項式の除法を暗算でする方法とは 大学入試数学の考え方と解法




多项式除法 维基百科 自由的百科全书




整式の除法です 丸をした所はどうやって計算したら xになるんです 高校 教えて Goo




多項式除法 多項式除法是除法的一種類型 俗稱長除 適用於整式除法 小數除 百科知識中文網


